Revision Notes on Practical Geometry
Line segment
A line segment is a part of a line with two endpoints.

A line perpendicular to a line segment
Any line which is perpendicular to a line segment makes an angle of 90°.

Construction of a line parallel to a given line, through a point not on the line
We need to construct it using ruler and compass only.
Step 1: Draw a line PQ and take a point R outside it.
Step 2: Take a point J on the line PQ and join it with R.
Step 3: Take J as a centre and draw an arc with any radius which cuts PQ at C and JR at B.
Step 4: Now with the same radius, draw an arc taking R as a centre.
Step 5: Take the measurement of BC with compass and mark an arc of the same measurement from R to cut the arc at S.
Step 6: Now join RS to make a line parallel to PR.

∠ARS = ∠BJC, hence RS ∥ PQ because of equal corresponding angles.
This concept is based on the fact that a transversal between two parallel lines creates a pair of equal corresponding angles.
Remark: This can be done by taking alternate interior angles instead of corresponding angles.
Construction of triangles
The construction of triangles is based on the rules of congruent triangles. A triangle can be drawn if-
Three sides are given (SSS criterion).
Two sides and an included angle are given (SAS criterion).
Two angles and an included side are given. (ASA criterion).
A hypotenuse and a side are given for right angle triangle (RHS criterion).
Construction of a triangle with three given sides (SSS criterion)
Example
Draw a triangle ABC with the sides AB = 6 cm, BC = 5 cm and AC = 9 cm.
Solution
Step 1: First of all draw a rough sketch of a triangle, so that we can understand how to go ahead.

Step 2: Draw a line segment AB = 6 cm.

Step 3: From point A, C is 9 cm away so take A as a centre and draw an arc of 9 cm.

Step 4: From point B, C is 5 cm away so take B as centre and draw an arc of 5 cm in such a way that both the arcs intersect with each other.

Step 5: This point of intersection of arcs is the required point C. Now join AC and BC.

ABC is the required triangle.
Construction of a triangle if two sides and one included angle is given (SAS criterion)
Example
Construct a triangle LMN with LM = 8 am, LN = 5 cm and ∠NLM = 60°.
Solution
Step 1: Draw a rough sketch of the triangle according to the given information.

Step 2: Draw a line segment LM = 8 cm.

Step 3: draw an angle of 60° at L and make a line LO.
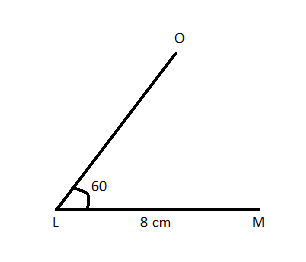
Step 4: Take L as a centre and draw an arc of 5 cm on LO.

Step 5: Now join NM to make a required triangle LMN.

Construction of a triangle if two angles and one included side is given (ASA criterion)
Example
Draw a triangle ABC if BC = 8 cm, ∠B = 60°and ∠C = 70°.
Solution
Step 1: Draw a rough sketch of the triangle.
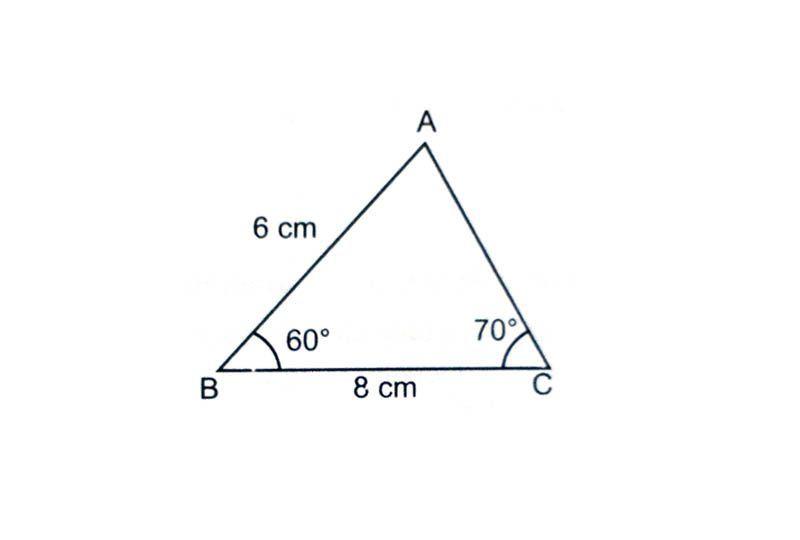
Step 2: Draw a line segment BC = 8 cm.

Step 3: Take B as a centre and make an angle of 60° with BC and join BP.

Step 4: Now take C as a centre and draw an angle of 70° using a protractor and join CQ. The point where BP and QC intersects is the required vertex A of the triangle ABC.

ABC is the required triangle ABC.
Construction of a right angle triangle if the length of the hypotenuse and one side is given (RHScriterion)
Example
Draw a triangle PQR which is right angled at P, with QR =7 cm and PQ = 4.5 cm.
Solution
Step 1: Draw a rough sketch of the triangle.

Step 2: Draw a line segment PQ = 4.5 cm.

Step 3: At P, draw PS ⊥ PQ. This shows that R must be somewhere on this perpendicular.

Step 4: Take Q as a centre and draw an arc of 7 cm which intersects PS at R.

PQR is the required triangle.
Contact Us
Welcome to www.fuzymail.co.in
Please email us if you have any queries about the site, advertising, or anything else.

We will revert you as soon as possible...
Thank you for contacting us!
Have a great day


.png)






No comments:
Post a Comment
thanks for your feedback