class 8 identity

Class 8 Maths Chapter 9 Identity
Syllabus of Class 8 Mathematics
1.Rational Numbers
2.Linear Equations in one variable
3.Understanding Quadrilaterals
4.Practical Geometry
5.Data Handling
6.Squares Square Roots
7.Cube and Cube Roots
8.Comparing Quantities
9.Algebraic Expressions and Identities
10.Visualising Solid Shapes
11.Mensuration
12.Exponents and Powers
13.Direct and Inverse Properties
14.Factorisation
15.Introduction to Graph
16.Playing with Numbers

Algebraic Expressions and Identities Class 8 Solutions

*Class 8 Maths YOUTUBE PLAYLIST videos containing more than 100+ videos

*Space and Science based knowledge PLAYLIST VIDEO containing 250 + videos

*Competitive examination for Science whole syllabus having videos more than 300+ videos

*Class 8 Maths Chapter 9 Identity STUDY MATERIAL PDF

Class 8 Maths Chapter 9 Notes - Algebric Expressions And Identities

Introduction to Algebraic expressions and identities

An algebraic expression is made up of constants, variables, and mathematical operations (addition, subtraction, multiplication and/or division). A constant is number whose value does not change, whereas the value of a variable changes. For example, x + 9 is an algebraic expression where 9 is a constant and x is a variable. Different elements like terms, factors and coefficients form these expressions.

Each part of an algebraic expression separated by a plus or minus sign is called a term of the algebraic expression.

Factors are the numbers and/or variables whose product make a term. If we look at the term 7x, it is the product of two factors 7 and x.

Coefficient is defined as the number that is multiplied by the other variables. In the term 11pqr, 11 is the coefficient of pqr.

An expression can be termed as monomial, binomial, trinomial, and polynomial based on the number of terms it has.

Monomial: It is an algebraic expression with only one term. For example, 9y is a monomial.

Binomial: It is an algebraic expression with two terms. For example, 2a – 6b is a binomial.

Trinomial: It is an algebraic expression with three terms. For example, 9a + 5b – c .

Polynomial: It is an algebraic expression that contains one or more terms consisting of constants and/or variables (whose exponents are non-negative integers). Monomials, binomials and trinomials come under the category of polynomials.

The terms of an algebraic expression can be categorised as like terms and unlike terms.

Like and Unlike Terms

Like Terms: If two or more terms have the same variable, then they are called like terms.

For example, 7x + 8x is an algebraic expression with like terms.

Unlike Terms: If two or more terms have different variables, they are called unlike terms.

For example, 7x + 8y is an algebraic expression with unlike terms.

We should understand how to select like and unlike terms because this helps us to add or subtract the terms of an algebraic expression. Let us see how we can do this.

NCERT Solutions for Class 8 Maths Chapter 9
Addition and Subtraction

While adding and subtracting two or more algebraic expressions, we first group the like terms. Then we add or subtract them using simple number rules.

If a and b are coefficients and x and y are variables, ax + bx + y = (a + b)x+ y.

If a and b are coefficients and x and y are variables, ax − bx + y = (a − b)x+ y.

Let us see an example.

Subtract x² + 3y² + 4xy – 4xyz from 9x² – 4y² + 7y + 2xy + 6.

9x² – 4y² + 7y + 2xy + 6

x² + 3y² + 4xy – 4xyz

– – – +

---------------------------------------------------

8x² – 7y² + 7y − 2xy + 6 + 4xyz

Multiplication

While multiplying algebraic expressions, every term of the first expression is multiplied with every term of the second expression. We have to follow some other steps as well.

Multiplying Like Terms

● The coefficients of the terms will get multiplied.

● The powers of the variables will not get multiplied, but added.

● Example: The product of 4x² and 9x will be 36x³.

Multiplying Unlike Terms

● The coefficients of the terms will get multiplied.

● The power will remain the same if the variables are different.

● If some of the variables are the same, then their powers will be added.

● Example: The product of xy, 4x, and 9xz will be 36x³yz.

Let’s see the multiplication of different types of algebraic expressions

Monomial by Monomial: If a and b are coefficients and x and y are variables, ax × bxy = abx²y.

Monomial by Binomial: If a and b are coefficients and x and y are variables, ax × (x + bxy) = ax²+ abx²y.

Monomial by Trinomial: If a and b are coefficients and x, y, and z are variables, ax × (x + by – z) = ax²+ abxy – axz.

Binomial by Binomial: If a and b are coefficients and x, y, and z are variables, (ax + y) × (x – z) = ax²– axz + xy − yz.

Binomial by Trinomial: If a and b are coefficients and x, y, and z are variables, (ax + y) × (x + by – z) = ax²+ abxy – axz.

Let us see an example.

Find the value of (p + 2q + r) × (2p – 3q).

(p + 2q + r) × (2p – 3q) = p (2p – 3q) + 2q (2p – 3q) + r (2p – 3q)

(p + 2q + r) × (2p – 3q) = p × 2p – p × 3q + 2q × 2p – 3q × 2q + r × 2p – r × 3q

(p + 2q + r) × (2p – 3q) = 2p²– 3pq + 4pq – 6q² + 2pr – 3qr

(p + 2q + r) × (2p – 3q) = 2p²+ pq – 6q²+ 2pr – 3qr

Equations contain an ‘equal to’ operator along with some other expressions. In an equation, if for every value of the variable, the value of the expression on the LHS is equal to the value of the expression on the RHS, then the equation is an identity. We will learn four standard identities that we generally use.

● (a + b)² = a² + 2ab + b²

● (a – b)² = a² – 2ab + b²

● (a + b)(a – b) = a² – b²

● (x + a)(x + b) = x² + (a + b)x + ab

Let us see an example where identities are used.

Find the value of (4x² + 4xy) (4x² + 3xy).

Using the identity: (x + a) (x + b) = x² + (a + b) x + ab
(4x² + 4xy) (4x² + 3xy)

= (4x²)² + (4xy + 3xy)(4x²) + 4xy × 3xy

= 16x⁴ + (16x³y + 12x³y) + 12x²y²

= 16x⁴+ 28x³y + 12x²y²

****************************************†**

*(a + b)2 = a2 + 2ab + b2

(a - b)2 = a2 - 2ab + b2
(a + b)(a - b) = a2 - b2
(x + a)(x + b) = x2 + (a + b)x + ab
(x + a)(x - b) = x2 + (a - b)x - ab
(x - a)(x + b) = x2 + (b - a)x - ab
(x - a)(x - b) = x2 - (a + b)x + ab
(a + b)3 = a3 + b3 + 3ab(a + b)
(a - b)3 = a3 - b3 - 3ab(a - b)

Question: 1 Give five examples of expressions containing one variable and five examples of expressions containing two variables.

Answer:

Five examples of expressions containing one variable are:

$x^{^{4}}, y, 3z, p^{^{2}}, -2q^{3}$

Five examples of expressions containing two variables are:

$x + y, 3p-4q,ab,uv^{2},-z^{2}+x^{3}$

Question: 2(i) Show on the number line.

$x$

Answer:

x on the number line:

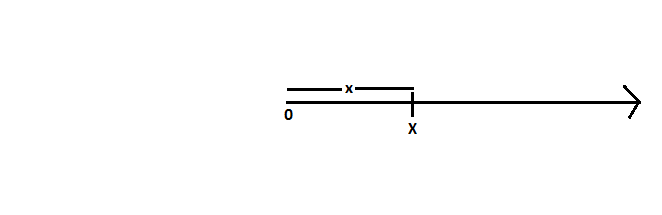
1643105164197

Question: 2(ii)

Show on the number line

$x-4$

Answer:

x-4 on the number line:

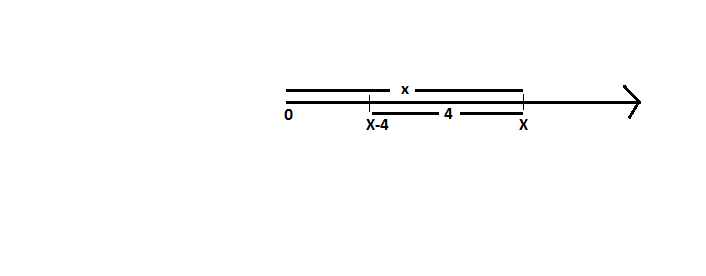
1643105231337

Question: 2(iii) Show on the number line

2x+1

Answer:

2x+1 on the number line:

c360_4-1

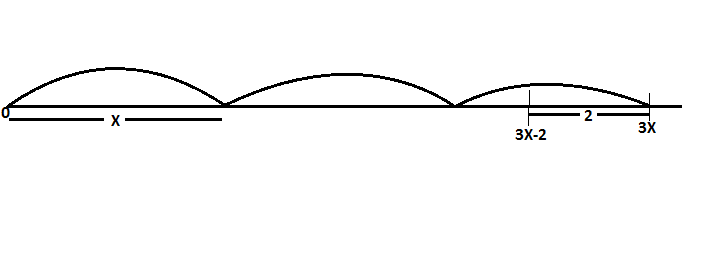
Question: 2(iv) Show on the number line

$3x-2$

Answer:

3x - 2 on the number line

1643105272368

Algebraic expressions and identities class 8 solutions - Topic 9.2 Terms, Factors and Coefficients

Question:1.Identify the coefficients of each term in the expression.

$x^2y^2-10x^2y+5xy^2-20$

Answer:

coefficient of each term are given below

$\\The\ coefficient\ of\ x^{2}y^{2}\ is \1\\ \\The\ coefficient\ of\ x^{2}y\ is \ -10\\ \\The\ coefficient\ of\ xy^{2}\ is \5\\$

Algebraic expressions and identities class 8 ncert solutions - Topic 9.3 Monomials, Binomials and Polynomials

Question: 1(i). Classify the following polynomials as monomials, binomials and trinomials.

$-z+5$

Answer:

Binomial since there are two terms with non zero coefficients.

Question: 1(ii) Classify the following polynomials as monomials, binomials and trinomials.

$x+y+z$

Answer:

Trinomial since there are three terms with non zero coefficients.

Question:1(iii) Classify the following polynomials as monomials, binomials and trinomials.

$y+z+100$

Answer:

Trinomial since there are three terms with non zero coefficients.

Question: 1(iv) Classify the following polynomials as monomials, binomials and trinomials.

$ab-ac$

Answer:

Binomial since there are two terms with non zero coefficients.

Question: 1(v) Classify the following polynomials as monomials, binomials and trinomials.

$17$

Answer:

Monomial since there is only one term.

Question: 2(a) constant 3 binomials with only $x$ as a variable;

Answer:

Three binomials with the only x as a variable are:

$\\ \\x+2,\ x +x^{2},\ 3x^{3}-5x^{4}$

Question: 2(b) constant 3 binomials with $x$ and $y$ as variables;

Answer:

Three binomials with x and y as variables are:

$\\ \\x+y,\ x-7y, xy^{2} + 2xy$

Question: 2(c) constant 3 monomials with $x$ and $y$ as variables;

Answer:

Three monomials with x and y as variables are

$\\ xy,\ 3xy^{4},\ -2x^{3}y^{2}$

Question: 2(d) constant 2 polynomials with 4 or more terms .

Answer:

Two polynomials with 4 or more terms are:

$a+b+c+d, x-3xy+2y+4xy^{2}$

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Topic 9.4 Like and Unlike Terms

Question:(i) Write two terms which are like

$7xy$

Answer:

$\\Two\ terms\ like\ 7xy\ are:\\ -3xy\ and\ 5xy$

Question:(ii) Write two terms which are like

$4mn^2$

Answer:

$\\Two\ terms\ which\ are\ like\ 4mn^{2}\ are:\\ mn^{2}\ and -3mn^{2.}$

we can write more like terms

Question:(iii) Write two terms which are like

$2l$

Answer:

$\\Two\ terms\ which\ are\ like\ 2l\ are:\\ l\ and\ -3l$

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities - Exercise: 9.1

Question:1(i) Identify the terms , their coefficients, for each of the following expressions

$5xyz^2-3zy$

Answer

following are the terms and coefficient

The terms are $5xyz^{2}\ and\ -3zy$ and the coefficients are 5 and -3.

Question: 1(ii) Identify the terms , their coefficients, for each of the following expressions

$1+x+x^2$

Answer:

the following is the solution

$\\The\ terms\ are\ 1,\ x,\ and\ x^{2}\ and\ the\ coefficients\ are\ 1,\ 1,\ and\ 1\ respectively.$

Question:1(iii)Identify the terms , their coefficients, for each of the following expressions

$4x^2y^2-4x^2y^2z^2+z^2$

Answer:

$\\The\ terms\ are\ 4x^{2}y^{2},\ -4x^{2}y^{2}z^{2}and\ z^{2}\ and\ the\ coefficients\ are\ 4,\ -4\ and\ 1\ respectively.$

Question: 1(iv) Identify the terms , their coefficients, for each of the following expressions

$3-pq+qr-rp$

Answer:

The terms are 3, -pq, qr,and -rp and the coefficients are 3, -1, 1 and -1 respectively.

Question:1(v) Identify the terms , their coefficients, for each of the following expressions

$\frac{x}{2}+\frac{y}{2}-xy$

Answer:

$\\The\ terms\ are\ \frac{x}{2},\ \frac{y}{2}\ and\ -xy\ and\ the\ coefficients\ are\ \frac{1}{2},\ \frac{1}{2}\ and\ -1\ respectively.$

Above are the terms and coefficients

Question: 1(vi) Identify the terms , their coefficients, for each of the following expressions

$0.3a-0.6ab+0.5b$

Answer:

The terms are 0.3a, -0.6ab and 0.5b and the coefficients are 0.3, -0.6 and 0.5.

Question: 2(a) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$x+y$

Answer:

Binomial.

Question: 2(b) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$1000$

Answer:

Monomial.

Question: 2(c) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$x+x^2+x^3+x^4$

Answer:

This polynomial does not fit in any of these three categories.

Question: 2(d)Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$7+y-5x$

Answer:

Trinomial.

Question: 2(e) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$2y-3y^2$

Answer:

Binomial.

Question: 2(f) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$2y-3y^2+4y^3$

Answer:

Trinomial.

Question: 2(g) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$5x-4y+3xy$

Answer:

Trinomial.

Question: 2(h) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$4z-15z^2$

Answer:

Binomial.

Question: 2(i) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$ab+bc+cd+da$

Answer:

This polynomial does not fit in any of these three categories.

Question:2(j) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$pqr$

Answer:

Monomial.

Question: 2(k) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$p^2q+pq^2$

Answer:

Binomial.

Question: 2(i) Classify the following polynomials as monomials, binomials,trinomi.Which polynomials do not fit any of these categories?

$2p+2q$

Answer:

Binomial.

Question: 3(i) Add the following

$ab-bc , bc -ca, ca-ab$

Answer:

ab-bc+bc-ca+ca-ab=0.

Question:3 (ii) Add the following

$a-b+ab, b-c+bc, c-a+ac$

Answer:

$\\a-b+ab+b-c+bc+c-a+ac\\ =(a-a)+(b-b)+(c-c)+ab+bc+ac\\ =ab+bc+ca$

Question:3 (ii)Add the following

$2p^2q^2-3pq+4, 5+7pq-3p^2q^2$

Answer:

$\\2p^{2}q^{2}-3pq+4+5+7pq-3p^{2}q^{2}\\ =(2-3)p^{2}q^{2} +(-3+7)pq +4+5\\ =-p^{2}q^{2}+4pq+9$

Question: 3(iv)Add the following

$l^2+m^2+n^2 , n^2+l^2, 2lm+2mn+2nl$

Answer:

$\\l^{2}+m^{2}+n^{2}+n^{2}+l^{2}+2lm+2mn+2nl\\ =2l^{2}+m^{2}+2n^{2}+2lm+2mn+2nl$

Question:1Find $4x\times 5y\times 7z$ First find $4x\times 5y$ and multiply it by $7z$ ; or first find $5y \times 7z$ and multiply it by $4x$ .

Answer:

$\\4x\times 5y\times 7z\\ =(4x\times 5y)\times 7z\\ =20xy\times 7z\\ =140xyz\\ \\4x\times 5y\times 7z\\ =(5y\times 7z)\times 4x\\ =35yz\times 4x\\ =140xyz$

We observe that the result is same in both cases and the result does not depend on the order in which multiplication has been carried out.

Class 8 maths chapter 9 question answer - exercise: 9.2

Question: 1(i) Find the product of the following pairs monomials

$4,7p$

Answer:

$4\times 7p=28p$

Question: 1(ii) Find the product of the following pairs monomials

$-4p,7p$

Answer:

$\\-4p\times 7p\\=(-4\times 7)p\times p\\=-28p^{2}$

Question: 1(iii) Find the product of the following pairs monomials

$-4p,7pq$

Answer:

$-4p\times 7pq\\=(-4\times 7)p\times pq\\=-28p^{2}q$

Question: 1(iv) Find the product of the following pairs monomials

$4p^3,-3p$

Answer:

$\\4p^{3}\times (-3p)\\ =4\times (-3)p^{3}\times p\\=-12p^{4}$

Question:1(v) Find the product of the following pairs monomials

$4p,0$

Answer:

$\\4p\times 0=0$

Question:2(A) Find the areas of rectangles with the followin pairs of monomials as their lengths and breadth respectively.

$(p,q)$

Answer:

The question can be solved as follows

$\\Area=length\times breadth\\ =(p\times q)\\ =pq$

Question:2(B)Find the areas of rectangles with the followin pairs of monomials as their lengths and breadth respectivi.

$(10m,5n)$

Answer:

the area is calculated as follows

$\\Area=length\times breadth\\ =10m\times 5n\\ =50mn$

Question:2(C) Find the areas of rectangles with the followin pairs of monomials as their lengths and breadth respectivi.

$(20x^2,5y^2)$

Answer:

the following is the solution

$\\Area=length\times breadth\\ =20x^{2}\times 5y^{2}\\ =100x^{2}y^{2}$

Question:2(D) Find the areas of rectangles with the followin pairs of monomials as their lengths and breadth respectivi.

$(4x,3x^2)$

Answer:

area of rectangles is

$\\Area=length\times breadth\\ =4x\times 3x^{2}\\ =12x^{3}$

Question:2(E) Find the areas of rectangles with the followin pairs of monomials as their lengths and breadth respectivi.

$(3mn,4np)$

Answer:

The area is calculated as follows

$\\Area=length\times breadth\\ =3mn\times 4np\\ =12mn^{2}p$

Question:3

Complete the table.

First monomial $\rightarrow$ Second monomial $\downarrow$	$2x$	$-5y$	$3x^2$	$-4xy$	$7x^2y$	$-9x^2y^2$
$2x$	$4x^2$	...	...	...	...	...
$-5y$	...	...	$-15x^2y$	...	...	...
$3x^2$	...	...	...	...	...	...
$-4xy$	...	...	...	...	...	...
$7x^2y$	...	...	...	...	...	...
$-9x^2y^2$	...	...	...	...	...	...

Answer:

First monomial $\rightarrow$ Second monomial $\downarrow$	$2x$	$-5y$	$3x^{2}$	$-4xy$	$7x^{2}y$	$-9x^{2}y^{2}$
$2x$	$4x^{2}$	$-10xy$	$6x^{3}$	$-8x^{2}y$	$14x^{3}y$	$-18x^{3}y^{2}$
$-5y$	$-10xy$	$25y^{2}$	$-15x^{2}y$	$20xy^{2}$	$-35x^{2}y^{2}$	$45x^{2}y^{3}$
$3x^{2}$	$6x^{3}$	$-15x^{2}y^{}$	$9x^{4}$	$-12x^{3}y$	$21x^{4}y$	$-27x^{4}y^{2}$
$-4xy$	$-8x^{2}y$	$20xy^{2}$	$-12x^{3}y$	$16x^{2}y^{2}$	$-28x^{3}y$	$36x^{3}y^{3}$
$7x^{2}y$	$14x^{3}y$	$-35x^{2}y^{2}$	$21x^{4}y$	$-28x^{3}y^{2}$	$49x^{4}y^{2}$	$-63x^{4}y^{3}$
$-9x^{2}y^{2}$	$-18x^{3}y^{2}$	$45x^{2}y^{3}$	$-27x^{4}y^{2}$	$36x^{3}y^{3}$	$-63x^{4}y^{3}$	$81x^{4}y^{4}$

Question:4(i) Obtain the volume of rectangular boxes with the following length, breadth and height respectfully.

$5a, 3a^2, 7a^4$

Answer:

$\\Volume=length\times breadth\times height\\ =5a\times 3a^{2}\times 7a^{4}\\ =15a^{3}\times 7a^{4}\\ =105a^{7}$

Question:4(ii)Obtain the volume of rectangular boxes with the following length, breadth and height respectfully.

$2p,4q,8r$

Answer:

the volume of rectangular boxes with the following length, breadth and height is

$\\Volume=length\times breadth\times height\\ =2p\times 4q\times 8r\\ =8pq\times 8r\\ =64pqr$

Question:4(iii) Obtain the volume of rectangular boxes with the following length, breadth and height respectfully.

$xy, 2x^2y, 2xy^2$

Answer:

the volume of rectangular boxes with the following length, breadth and height is

$\\Volume=length\times breadth\times height\\ =xy\times 2x^{2}y\times 2xy^{2}\\ =2x^{3}y^{2}\times 2xy^{2}\\ =4x^{4}y^{4}$

Question:4(iv) Obtain the volume of rectangular boxes with the following length, breadth and height respectfully.

$a, 2b, 3c$

Answer:

the volume of rectangular boxes with the following length, breadth and height is

$\\Volume=length\times breadth\times height\\ =a\times 2b\times 3c\\ =2ab\times 3c\\ =6abc$

Question:5(i) Obtain the product of

$xy,yz,zx$

Answer:

the product

$\\xy\times yz\times zx\\ =xy^{2}z\times zx\\ =x^{2}y^{2}z^{2}$

Question:5(ii)Obtain the product of

$a,-a^2,a^3$

Answer:

the product

$\\a\times (-a^{2})\times a^{3}\\ =-a^{^{3}}\times a^{3} =-a^{6}$

Question:5(iii)Obtain the product of

$2,\ 4y,\ 8y^{2},\ 16y^{3}$

Answer:

the product

$\\2\times 4y\times 8y^{2}\times 16y^{3}\\ =8y\times 8y^{2}\times 16y^{3}\\ =64y^{3}\times 16y^{3}\\ =1024y^{6}$

Question:5(iv) Obtain the product of

$a, 2b, 3c, 6abc$

Answer:

the product

$\\a\times 2b\times 3c\times 6abc\\ =2ab\times 3c\times 6abc\\ =6abc\times 6abc\\ =36a^{2}b^{2}c^{2}$

Question:5(v) Obtain the product of

$m, -mn, mnp$

Answer:

the product

$\\m\times (-mn)\times mnp\\ =-m^{2}n\times mnp\\ =-m^{3}n^{2}p$

Class 8 maths chapter 9 NCERT solutions - Topic 9.8.1 Multiplying a Monomial by a Binomial

Question:(i) Obtain the product of

$2x(3x+5xy)$

Answer:

Using distributive law,

$2x(3x + 5xy) = 6x^2 + 10x^2y$

Question:(ii)Obtain the product of

$a^2(2ab-5c)$

Answer:

Using distributive law,

We have : $a^2(2ab-5c) = 2a^3b - 5a^2c$

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities - Topic 9.8.2 Multiplying A Monomial By A Trinomial

Question:1Obtain the product of

$(4p^2+5p+7)\times 3p$

Answer:

By using distributive law,

$(4p^2+5p+7)\times 3p = 12p^3 + 15p^2 + 21p$

Class 8 maths chapter 9 NCERT solutions - exercise: 9.3

Question:1(i) Carry out the multiplication of the expressions in each of the following pairs

$4p, q+r$

Answer:

Multiplication of the given expression gives :

By distributive law,

$(4p)(q+r) = 4pq + 4pr$

Question1(Ii)Carry out the multiplication of the expressions in each of the following pairs

$ab, a-b$

Answer:

We have ab, (a-b).

Using distributive law we get,

$ab(a-b) = a^2b - ab^2$

Question:1(iii) Carry out the multiplication of the expressions in each of the following pairs

$a+b, 7a^2b^2$

Answer:

Using distributive law we can obtain multiplication of given expression:

$(a + b)(7a^2b^2) = 7a^3b^2 + 7a^2b^3$

Question:1(iv) Carry out the multiplication of the expressions in each of the following pairs

$a^2-9,4a$

Answer:

We will obtain multiplication of given expression by using distributive law :

$(a^2 - 9 )(4a) = 4a^3 - 36a$

Question:1(v) Carry out the multiplication of the expressions in each of the following pairs

$pq+qr+rp, 0$

Answer:

Using distributive law :

$(pq + qr + rp)(0) = pq(0) + qr(0) + rp(0) = 0$

Question:2 Complete the table

	First expression	Second expression	Product
(i)	$a$	$b+c+d$	...
(ii)	$x+y-5$	$5xy$	...
(iii)	$p$	$6p^2-7p+5$	...
(iv)	$4p^2q^2$	$p^2-q^2$	...
(v)	$a+b+c$	$abc$	...

Answer:

We will use distributive law to find product in each case.

	First expression	Second expression	Product
(i)	$a$	$b+c+d$	$ab + ac+ ad$
(ii)	$x+y-5$	$5xy$	$5x^2y + 5xy^2 - 25xy$
(iii)	$p$	$6p^2-7p+5$	$6p^3 - 7p^2 + 5p$
(iv)	$4p^2q^2$	$p^2-q^2$	$4p^4q^2 - 4p^2q^4$
(v)	$a+b+c$	$abc$	$a^2bc + ab^2c + abc^2$